Ketika mendengar lingkaran, apa yang ada di pikiran Anda? Pastinya yang terbesit adalah kancing, ban sepeda, atau pizza ya?
Lingkaran adalah bangun datar yang terdiri dari himpunan titik-titik yang berjarak sama terhadap suatu titik tertentu, dimana titik tertentu tersebut dinamakan titik pusat lingkaran. Sedangkan, jarak dari pusat ke setiap titik disebut dengan jari-jari.
Unsur – Unsur Lingkaran
Ada beberapa unsur dalam sebuah lingkaran, antara lain:
1. Titik Pusat
Titik pusat adalah titik yang terletak di tengah-tengah lingkaran.
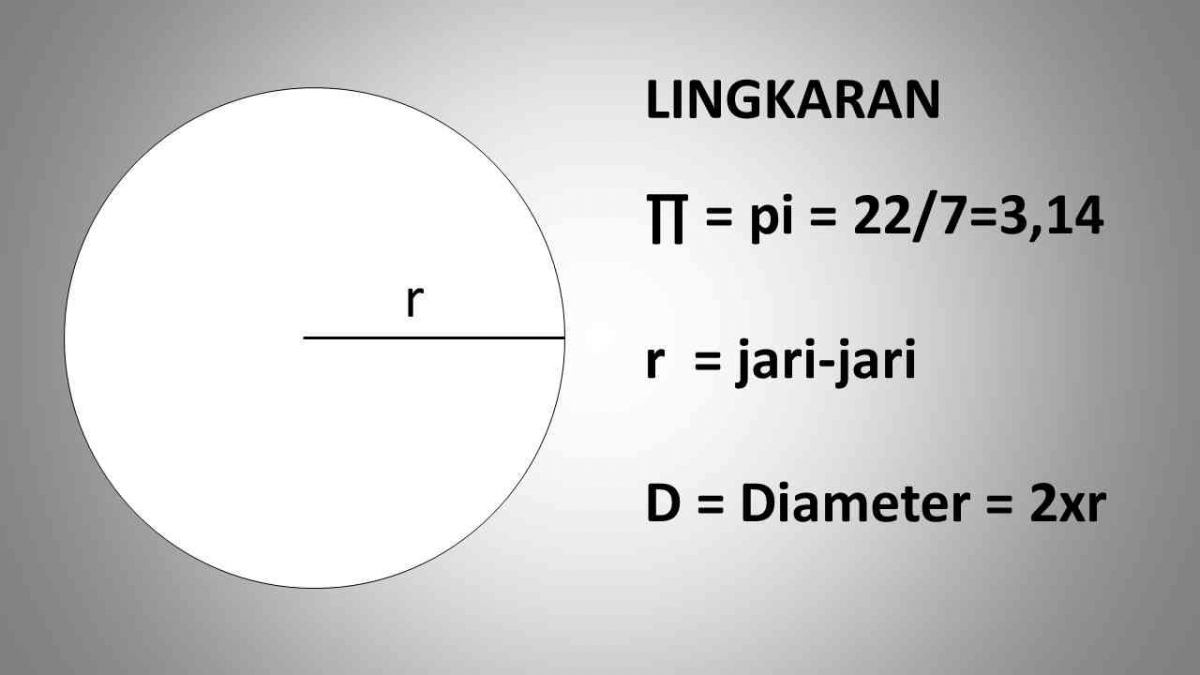
2. Jari-jari (r)
Jari-jari lingkaran adalah garis dari titik pusat lingkaran ke lengkungan lingkaran.
3. Diameter
Diameter adalah garis lurus yang menghubungkan dua titik pada lengkungan lingkaran dan melalui titik pusat.
4. Busur
Busur adalah garis lengkung yang terletak pada lengkungan lingkaran dan menghubungkan dua titik sebarang di lengkungan tersebut.
5. Tali Busur
Tali busur adalah garis lurus dalam lingkaran yang menghubungkan dua titik pada lengkungan lingkaran.
6. Tembereng
Tembereng adalah luas daerah dalam lingkaran yang dibatasi oleh busur dan tali busur.
7. Juring
Juring lingkaran adalah luas daerah dalam lingkaran yang dibatasi oleh dua buah jari-jari lingkaran dan sebuah busur yang diapit oleh kedua jari-jari lingkaran.
9. Apotema
Apotema adalah garis yang menghubungkan titik pusat lingkaran dengan tali busur lingkaran tersebut.
Rumus Luas Lingkaran
Nah setelah mengetahui unsur-unsur lingkaran, selanjutnya adalah membahas tentang rumus luas lingkaran, rumus keliling lingkaran beserta contoh soalnya.
L = π x r2, dengan π = konstanta pi (3,14 atau 22/7), dan r = jari-jari lingkaran.
Rumus Keliling Lingkaran
Sedangkan rumus keliling lingkaran adalah 2 x π x r.
Jari-jari lingkaran adalah setengah dari diameter lingkaran.
Sehingga luas dan keliling lingkaran juga dapat menggunakan rumus
Luas lingkaran = 1/4 x pi x d2
Keliling lingkaran = π x d
Dimana d = diameter lingkaran
Contoh Soal Cara Menghitung Luas dan Keliling Lingkaran
Soal 1
Sebuah lingkaran memiliki jari-jari 7 cm. Hitungkah luas dan keliling lingkaran tersebut?
Jawaban:
Diketahui: r = 7 cm
Luas Lingkaran:
L = π x r2
L = 22/7 x 72
L = 154 cm2
Keliling Lingkaran:
Keliling = 2 x π x r
Keliling = 2 x 22/7 x 7
Keliling = 44 cm
Jadi, luas lingkaran tersebut adalah 154 cm2 dan kelilingnya adalah 44 cm.
Contoh soal 2
Diketahui ada sebuah lingkaran yang mempunyai diameter 40 cm. Berapakah luas dan keliling lingkaran tersebut?
Jawaban:
d = 40 cm
r = d/2 = 20 cm
Luas Lingkaran:
L = π x r2
L = 22/7 x 202
L = 1256 cm2
Keliling Lingkaran:
Keliling = 2 x π x r
Keliling = 2 x 22/7 x 20
Keliling = 127 cm
Jadi, luas lingkaran tersebut adalah 1256 cm2 dan kelilingnya adalah 127 cm.
Soal 3
Ada sebuah lingkaran mempunyai diameter 20. Berapakah luas dan keliling lingkaran tersebut?
Jawaban:
d = 20 cm
r = d/2 = 10 cm
Luas Lingkaran:
L = π x r2
L = 22/7 x 102
L = 314 cm2
Contoh soal 4
Ada sebuah karet gelang berbentuk lingkaran mempunyai diameter 28 cm. Tentukan luas dan keliling lingkaran tersebut!
L = 1/4 x pi x d2
= 1/4 x 22/7 x 282
= 616 cm2
K = π x d
= 22/2 x 28
= 88 cm